2022-10-06数字图像处理 0次访问

Signal Processing

剧集推荐📺：
《仁医》，只能说是穿越剧的天花板了🫡🫡🫡

由于连续函数的性质，它们不能在计算机上直接表示出来。表示连续函数最有用的方法之一是使用函数的样本，即只需要将函数的值存储在许多不同的点上，并在需要它们的时候重构它们之间的值。例如被数码相机捕获的图像就是这样的一种采样表示，相机将镜头捕捉的2维连续坐标到颜色集合的映射函数转换成 2维离散坐标到颜色集合的映射函数。

图像中常见的artifacts：锯齿和摩尔纹。

aliasing产生的原因：采样率不够，原本的高频信号被认为是低频信号。

sampling & reconstruction

将‘离散世界’和‘连续世界’连接在一起的方式：

sampling：通过仅保留函数在所有整数参数处的值，而忽略其它位置的值将连续函数转换为离散的形式。
reconstruction：将离散函数或序列转换成连续函数。可以通过离散-连续卷积来实现该操作。

Resampling

resampling：更改采样率或更改图像大小。具体来说当以resampling操作的角度来实现这两个功能时，收先会从离散的图片重构出原始的连续图像信号，然后对重构出的信号再进行采样得到改变大小后的图片。

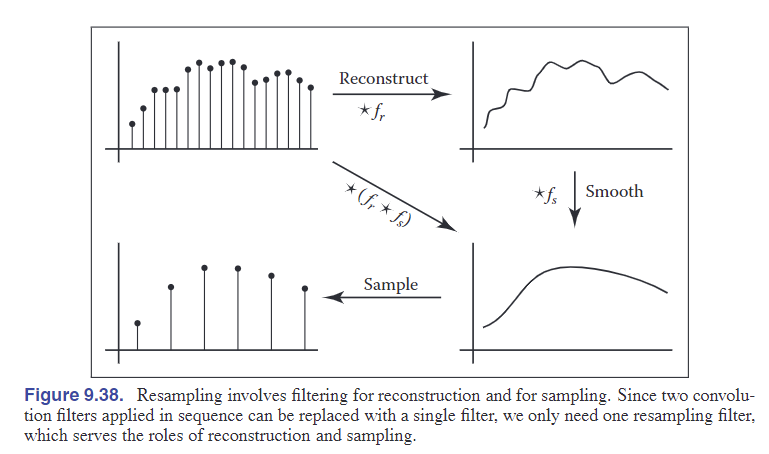
如上图所示，resampling filter包括reconstruction filter和sampling filter。因此只需要用一个resampling filter和输入图片进行连续-离散卷积即可得到resampling之后的结果：（下图是1D信号（假设是只有一行的像素条）的resampling操作伪码）

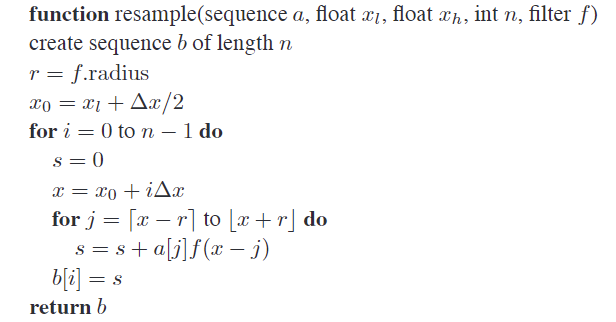
输入a是原始序列，xl,xh是a序列的两个边界（因此$x_l+\Delta x/2$是第一个采样点），n是resample后新的序列b的长度，f是resampling filter。

对于边界情况，可以这样处理：即将filter除以落在图片上这一部分的和，这样在这些重新归一化的样本上filter将保持和为1。

resampling filter如何选择？
即要考虑的是如何决定filter的形状和大小。
由于resampling filter是reconstruction filter和sampling filter的结合，因此两者对filter的要求将会影响resampling filter的选择。对于reconstruction来说，一个filter要足够的光滑以避免放大图片时aliasing artifacts的出现；对于sampling来说，filter要足够的大避免欠采样，并且要足够光滑避免摩尔纹。
选择哪一种filter（形状）？
这是权衡执行速度和质量之后的结果，例如当非常在意执行速度时选择box filter，质量和速度均衡则选择tent filter，质量更加重要则可以选择piecewise cubic的filter。
filter大小的选择？
当决定好filter的形状之后，根据输入和输出图片之间的相对分辨率小的那个来决定其大小。当对图片做下采样操作时（把图片缩小），此时相比于reconstruction，sampling更加重要（根据下面的频域知识可以知道，当缩小图片时相当于采样率降低，此时复制频谱之间距离会更近，因此采样此时更重要，需要更smooth的filter来截断高频防止混叠的发生），此时采用输出图片像素之间的间隔来作为filter的大小（例如输入图片的像素间隔为1，在缩小3倍后，那么像素之间的间隔就变为了3，所以以将filter放大3倍）。
当放大图片时，像素之间的间隔将会变小，采样率提高sample的效果提升，因此reconstruction占据主导，此时不需要再额外的去缩放filter了否则可能会影响到原始信号的恢复，直接使用输入图片之间样本的间隔大小作为filter的缩放比例即可。

Fourier Transform

逆傅里叶变换（IFT）：
$$
f(x) = \int _ {-\infty }^ {+\infty } \hat{f}(u)e^{2\pi iux}du
$$
如上$\hat{f}$是一个关于频率$u$的函数，它被称为$f$的傅里叶变换（注意Fourier transform这个词同时既可代指函数$\hat{f}$，也可以代指下面的FT操作），它相当于一个权重项，说明了如何将很多正弦曲线累积起来构造原始的函数$f$。$\hat{f}$的magnitude称为Fourier spectrum。
傅里叶变换（FT）：
$$
\hat{f}(u) = \int _ {-\infty }^ {+\infty } f(x)e^{-2\pi iux}dx
$$
我们将f的傅里叶变换操作记为$\mathcal{F}${$f$}，逆傅里叶变换记为$ \mathcal{F} ^{-1}$ {$\hat{f}$}。

一些性质

函数和它的傅里叶变换有相同的平方积分：
$$
\int (f(x))^2dx = \int (\hat{f}(u))^2du
$$
从物理角度来说，这意味着它们有着相同的能量。
把一个函数放大a倍，那么同样的其傅里叶变换也被放大a倍：$\mathcal{F}$ {$af$} = $a \mathcal{F}${$f$}
把一个函数沿着x轴拉伸其傅里叶变换会沿着u轴被挤压相同的大小:$\mathcal{F}$ {$f(x/b)$} = $b\hat{f}(bx)$。之所以给傅里叶变换乘b，是为了保证能量相同。
$f$的平均值等于$\hat{f}(0)$，$\hat{f}(0)$是信号0频率处的分量，也可以被称为DC分量。
卷积和傅里叶变换：$\mathcal{F}${$f \star g$}$ = \hat{f}\hat{g}$，$\hat{f} \star \hat{g}$$ =\mathcal{F}${$fg$}

不同filter的傅里叶变换

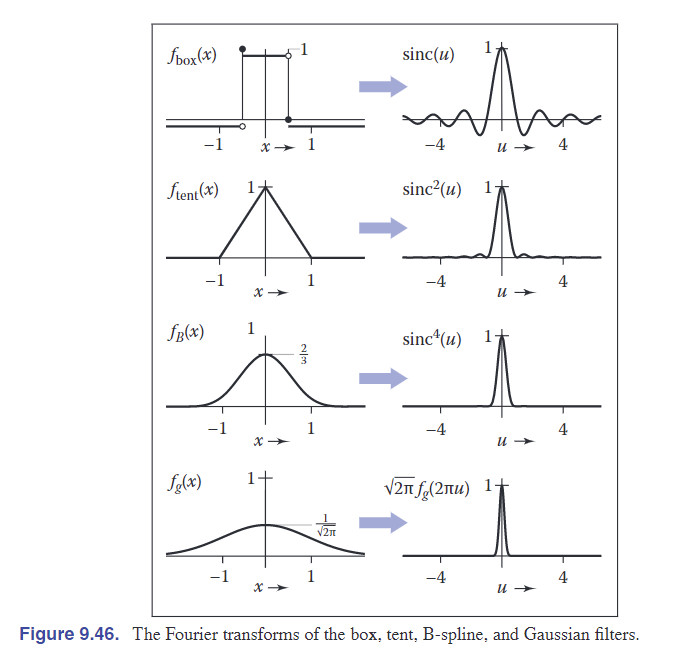
注意：函数$\frac{sin x}{x}$记为$sinc x$。

Dirac Impulses in Sampling Theory

采样具有位置和值，通过将impulse 移动到采样位置并根据该位置的函数值进行缩放来表示一个采样。在a位置具有值b的采样可以被表示为$b\delta(x-a)$，类似的在一点a采样函数$f(x)$可以被表示为$f(a)\delta(x-a)$。
因此，在一系列等距点处对函数进行采样表示为将函数乘以一系列等距impulse的总和，称为impulse train，因此具有周期 T 的impulse train表示为：
$$
s_T(x) = \sum _{i=-\infty} ^{\infty} \delta(x-Ti)
$$

性质：一个以T为周期的impulse train，其傅里叶变换是以1/T为周期的impulse train。

Sampling and Aliasing

补充：连续信号的傅里叶变换包含任意的频率分量，对于大多数的信号特别是图片来说，随着频率的升高，其包含的内容会不断的下降，其中0频率部分含有内容信息最多。

采样（sampling）一个信号，即将该信号和impulse train相乘即可，因此采样后的信号为$fs_T$，根据傅里叶变换的性质，时域函数相乘对应于频域二者做卷积，即$\hat{f} \star \hat{s_T} = \hat{f} \star s_{1/T}$，因此可得到下面的式子：
$$
(\hat{f} \star s_{1/T})(u)=\sum _{i=-\infty} ^{\infty} \hat{f}(u-i/T)
$$

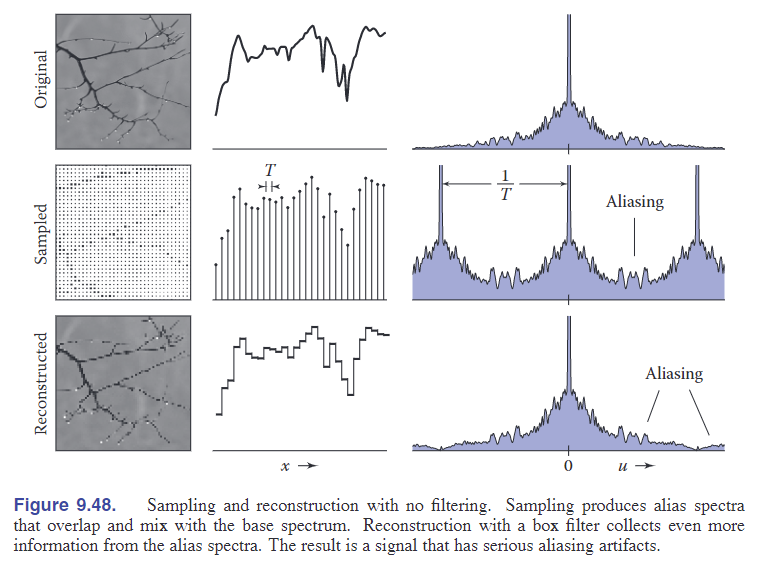
因此从上式可以看到，$\hat{f}$与impulse train卷积会生成一系列等距的$f$的谱(spectrum)（$\hat{f}$）的副本。原始的spectrum称为 base spectrum，复制品称为alias spectra。

可以发现，如果采样频率相差整数倍，那采样后的结果是无法区分的，它们将会产生相同的样本。
如果信号频谱的这些副本重叠，那么不同频率的信息之间将会互相融合产生混叠（aliasing）现象。
副本之间何时重叠？当信号包含超过采样率一半的频率成分时，则副本间会发生重叠。

对于重建（reconstruction），之前把它视为了一个离散-连续卷积操作，其实这和box filter（假设这里使用box filter来重建信号）与具有表示样本的一系列脉冲的连续卷积相同，因此根据卷积乘法性质可知重建信号的频谱将是采样信号的频谱和box filyer频谱的乘积。
从上面box filter的傅里叶变换可以看出，box filter在很大的范围内都有值，因此它衰减采样信号的alias spectra并不充分，因此会产生由重建引起的aliasing，其在图像中表现为正方形的图案。

Preventing Aliasing

Sampling

在采样的时候使用低通滤波器 ：这样可以限制信号的频率范围，以便alias spectra不会和base spectrum发生重叠（也即副本之间不发生重叠）。【用低通滤波器对信号进行卷积可以使频谱变窄到足以消除重叠。虽然已经失去了高频，但这比让它们被信号打乱变成伪影要好。】
使用更高的采样频率：更高的采样率可以让alias spectra离base spectrum更远。
那该采用什么样的采用率呢？根据Nyquist–Shannon(奈奎斯特-香农)采样定理：如果一个系统以超过信号最高频率至少两倍的速率对模拟信号进行均匀采样，那么原始模拟信号就能从采样产生的离散值中完全恢复。

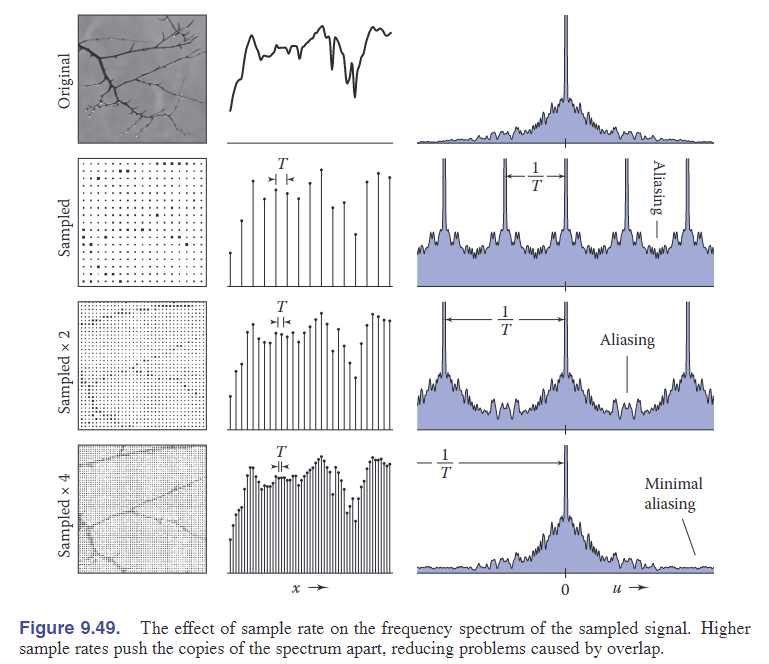
注意：对于特定信号如果具有足够高的采样率，我们不需要使用采样滤波器。但是如果信号包含很宽频率范围（例如其中有锐利边缘的图像），则必须使用采样滤波器对信号进行带宽限制，然后才能对其进行采样。

Reconstruction
reconstruction filter的作用是在保留base spectrum的同时去除alias spectra。
合理的重构滤波器的一个特征：在采样频率的所有倍数的频率空间中都为零，即在时域中具有ripple-free的性质。
因此，一个好的重构滤波器需要是一个好的低通滤波器，另外还需要完全阻断所有采样频率的倍数。即更彻底的消除alias spectra，减少高频伪影泄漏到重构信号中，同时尽可能少地干扰base spectrum。

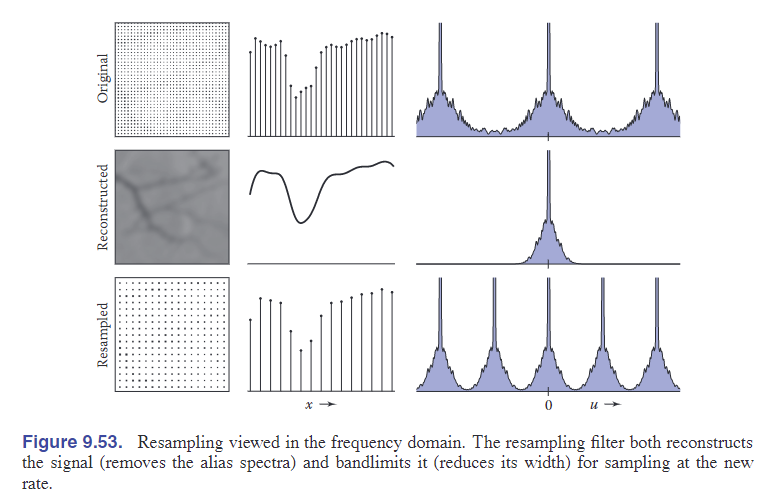
Resampling
重采样滤波器必须去除混叠光谱并使光谱足够窄，以便以新的采样率进行采样。